Simple planar undulator

Basic example of computation of the field emitted by an undulator of a synchrotron light source.

Import modules required for simulations

import matplotlib.pyplot as plt
import numpy as np

import pysrw as srw

We take as example the parameters of an undulator installed in a light source (ALBA-Spain, NCD beamline)

energy = 3.0        # GeV
lambda_u = 0.0216   # m
N_u = 92
B_0 = 0.75          # T

The magnet is created with the default SRW model for planar undulators

und = srw.magnets.UndulatorPlanar(energy=energy,
                                  undPeriod=lambda_u, numPer=N_u,
                                  magField=B_0)

The deflection parameter and fundamental harmonic of such undulator are

K = und.getK()
lambda_1 = und.getLambda1()
print(f"Deflection parameter: {K:.2f}")
print(f"Fundamental harmonic: {lambda_1:.2f} nm")

Deflection parameter: 1.51
Fundamental harmonic: 0.67 nm

The magnetic element must be included in a magnetic container. In this simple example, the dipole is the only device and the limits for the numerical integration as left as default.

mag_container = srw.magnets.MagnetsContainer([und], lengthPadFraction=2)

The last input for the simulation is the emitter, instance of ParticleBeam()

beam = srw.emitters.ParticleBeam(energy, xPos=0, yPos=0, zPos=-1.5)

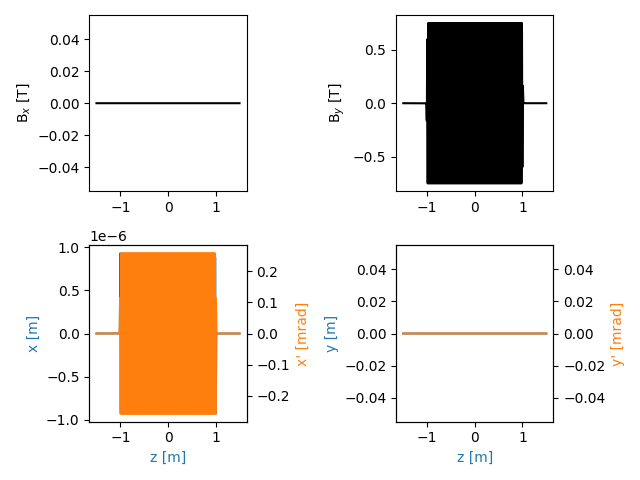
Before computing the wavefront, it is a good practice to obtain and plot the particle trajectory and check that the simulation objects properly defined

traj = srw.computeTrajectory(beam, mag_container, sStart=0, sEnd=3)
srw.plotTrajectory(traj)

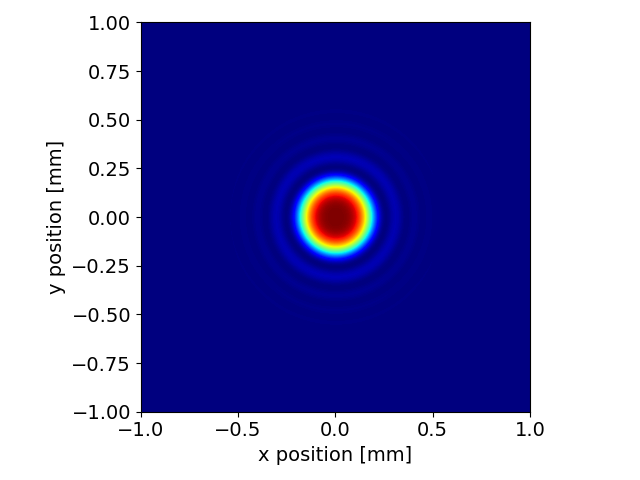
Create a 10 mm x 10 mm observation mesh, with a resolution of 100 um, placed 1 m downstream of the source

observer = srw.wavefronts.Observer(centerCoord=[0, 0, 10],
                                   obsXextension=2e-3,
                                   obsYextension=2e-3,
                                   obsXres=5e-6,
                                   obsYres=5e-6)

We can finally simulate the wavefront and derive the optical intensity, for example at the fundamental harmonics.

wl = lambda_1
wfr = srw.computeSrWfrMultiProcess(4, particleBeam=beam,
                                   magnetsContainer=mag_container,
                                   observer=observer, wavelength=wl)
intensity = wfr.getWfrI()
srw.plotI(intensity)

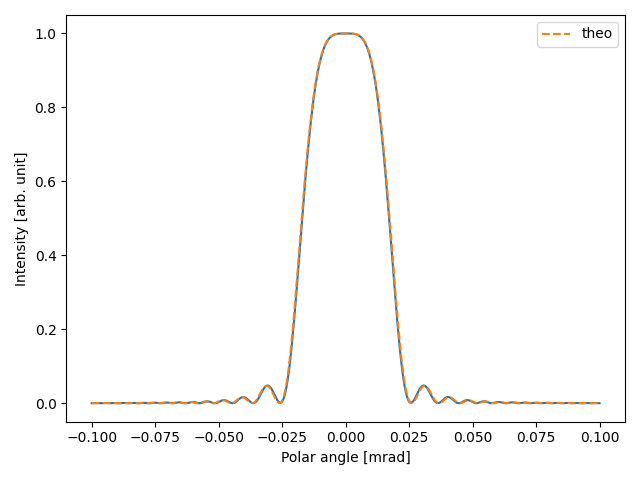
The distribution of SR emitted by a particle in a uniform field has an analytical expression. Let’s compare it to the simulation result. We extract a vertical slice from the simulation radiation

cuts = srw.extractCrossCuts(intensity)
yax = cuts["yax"]
int_srw = cuts["ydata"]

and compute the theoretical distribution for undulator radiation (tuned at fundamental wavelength) as

r_p = observer.zPos
theta = np.arctan(yax / r_p)
gamma = beam.nominalParticle.gamma

e_theo = np.sinc((theta**2 / 2 * (N_u * lambda_u) / (wl*1e-9)))
int_theo = e_theo**2

Simulated and theoretical distributions are finally plotted

fig, ax = plt.subplots()
ax.plot(theta*1e3, int_srw / np.max(int_srw))
ax.plot(theta*1e3, int_theo  / np.max(int_theo), label="theo", linestyle="--")
ax.set_xlabel("Polar angle [mrad]")
ax.set_ylabel("Intensity [arb. unit]")
ax.legend()
plt.show()
plt.tight_layout()

Estimated memory usage: 11 MB